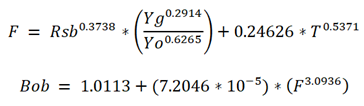Como ya es costumbre, ahora se muestra la
aplicación de las correlaciones de la entrada “Factor de volumen del Aceite”, para
mostrar la utilidad se considera una presión de burbuja de 2500 psi, una
temperatura de 180 °F, con una densidad API de 31 y una densidad del gas de
0.95 y una compresibilidad de 9.62*10^-6.
Las
correlaciones que se muestran a continuación, utilizan la presión de burbuja
por ello se tiene Rsb, si se desea obtener el factor de volumen por arriba o
por debajo de la presión de burbuja se deben de obtener la Rs a las condiciones deseadas.
import
numpy as np
PB =
2500
T =
180
API
= 31
Yg =
0.95
Co =
9.62*10**-6
Yo =
141.5/(API+131.5)
#
Correlación de Standing, M.B.
Rsb
= 671.0104
F =
Rsb*(np.sqrt(Yg/Yo))+1.25*T
Bob1
= 0.9759+12*10**-5*F**1.2
#
Correlación de Vázquez, M.E. y Beggs, H.D.
Rsb
= 581.9883
if
API <= 30:
C1 = 4.677*10**-4
C2 = 1.751*10**-5
C3 = -1.8106*10**-8
elif
API > 30:
C1 = 4.670*10**-4
C2 = 1.100*10**-5
C3 = 1.3370*10**-9
Bob2
= 1+(C1*Rsb)+C2*(T-60)*(API/Yg)+C3*Rsb*(T-60)*(API/Yg)
#
Correlación de Glaso, O.
Rsb
= 559.536
F =
Rsb*((Yg/Yo)**0.526)+0.968*T
Bob3
= 1+10**(-6.58511+2.91329*np.log10(F)-0.27683*(np.log10(F)**2))
#
Correlación de la TOTAL, C.F.P.
Rsb
= 688.7342
Bob4
=
1.022+(4.857*10**-4*Rsb)-2.009*10**-6*(T-60)*(API/Yg)+17.569*10**-9*Rsb*(T-60)*(API/Yg)
#Correlación
de Al-Marhoun, M.A.
Rsb
= 841.1555
F =
(Rsb**0.74239)*(Yg**0.323294)*(Yo**-1.20204)
Bob5
=
0.497069+((0.862963*10**-3)*(T+460))+((0.182594*10**-2)*F)+((0.318099*10**-5)*F**2)
#
Correlación de Dokla, M.E. y Osman, M.E.
Rsb
= 881.8047
F =
(Rsb**0.773572)*(Yg**0.40402)*(Yo**-0.882605)
Bob6
= (0.431935*10**-1)+((0.156667*10**-2)*(T+460))+((0.139775*10**-2)*F)+(0.380525*10**-5)*(F**2)
#
correlación de Petrosky, G.E., Jr. y Farshad, F.F.
Rsb
= 623.9002
F =
Rsb**0.3738*((Yg**0.2914)/(Yo**0.6265))+0.24626*T**0.5371
Bob7
= 1.0113+(7.2046*10**-5)*(F**3.0936)
#
Correlación de Kartoatmodjo, T. y Schmidt, Z.
Rsb
= 555.4992
F =
Rsb**0.755*Yg**0.25*Yo**-1.5+0.45*T
Bob8
= 0.9846+(1*10**-4)*(F**1.5)
# La
presión está por encima de la presión de burbuja.
“””Aquí
se muestra como se obtiene el factor de volumen del aceite a una
presión de 3000 psi, como está por arriba de la presión de burbuja se considera
que solo afecta la compresibilidad del aceite, en este caso tomamos la correlación
de Glaso, O.”””
P =
3000
Rsb
= 559.536
F =
Rsb*((Yg/Yo)**0.526)+0.968*T
Bob
= 1+10**(-6.58511+2.91329*np.log10(F)-0.27683*(np.log10(F)**2))
Bo =
Bob*np.exp(Co*(PB-P))
print("""El
resumen de resultados es:
Standing, M.B
---------------------------------
"""+str(round(Bob1,4))+"""
Vásquez, M.E. y Beggs, H.D.
------------------- """+str(round(Bob2,4))+"""
Glaso, O.
-------------------------------------
"""+str(round(Bob3,4))+"""
TOTAL, C.F.P.
---------------------------------
"""+str(round(Bob4,4))+"""
Al-Marhoun, M.A.
------------------------------ """+str(round(Bob5,4))+"""
Dokla, M.E. y Osman, M.E.
--------------------- """+str(round(Bob6,4))+"""
Petrosky, G.E., Jr. y Farshad, F.F.
----------- """+str(round(Bob7,4))+"""
Kartoatmojo, T. y Schmidt, Z.
----------------- """+str(round(Bob8,4))+"""
La presión está por encima de la de
burbuja --- """+str(round(Bo,4) ))
El
resumen de resultados es:
Standing, M.B
--------------------------------- 1.4115
Vásquez, M.E. y Beggs, H.D.
------------------- 1.3179
Glaso, O. -------------------------------------
1.3237
TOTAL, C.F.P.
--------------------------------- 1.396
Al-Marhoun, M.A.
------------------------------ 1.4586
Dokla, M.E. y Osman, M.E.
--------------------- 1.5076
Petrosky, G.E., Jr. y Farshad, F.F.
----------- 1.3878
Kartoatmojo, T. y Schmidt, Z.
----------------- 1.3209
La presión está por encima de la de
burbuja --- 1.3173
[Finished
in 391ms]